一、缺失数据的产生机制
在抽样调查中,经常会遇到调查问卷中某些项目没有回答的情况,这就是数据缺失的问题。数据缺失问题无论是在市场调查、政府调查还是学术调查中都呈现越来越严重的趋势。这是由多种原因造成的。首先,公民越来越重视个人的隐私权,不愿意透露一些个人信息;其次,不规范的市场调查影响了调查的严肃性,使得受访者对各类调查不屑一顾,不能认真对待;第三,问卷设计不规范,问卷内容过长或过难,尤其是市场调查中的各类“搭车调查”使得问卷过长,造成受访者的厌倦心理;第四,调查主办单位不重视访问员的培训,访问员缺乏一些必备的追问、补问、查漏等基本技巧。
缺失数据根据其产生机制可以分为完全随机缺失(MCAR)、随机缺失(MAR)和非随机缺失(MNAR)。完全随机缺失是指这样一种情况:缺失情况相对于所有可观测和不可观测的数据来说,在统计学意义上是独立的。比如说,受访者在街头接受访问时,突然沙粒吹进了眼睛导致问卷后面的问题无法回答,从而造成了数据缺失。随机缺失是一个观测出现缺失值的概率是由数据集中不含缺失值的变量决定的,而不是由含缺失值的变量决定的。非随机缺失是与缺失数据本身存在某种关联,比如问题设计过于敏感造成的缺失。
识别缺失数据的产生机制是极其重要的。首先这涉及到代表性问题。从统计上说,非随机缺失的数据会产生有偏估计,因此不能很好地代表总体。其次,它决定数据插补方法的选择。随机缺失数据处理相对比较简单,但非随机缺失数据处理比较困难,原因在于偏差的程度难以把握。
缺失数据的插补是指选择合理的数据代替缺失数据。不同的插补法对总体推断会产生较大的影响,尤其是在缺失数量较大的情况下。目前国内学者对缺失数据的插补问题尚未有充分的认识。笔者发现,研究者在抽样调查报告中很少会说明缺失值的处理方法,但事实上,绝大部分社会科学调查(包括市场调查)都会包含不完整的数据,理应对此有所说明。
二、几种常见的缺失数据插补方法
(一)个案剔除法(Listwise Deletion)
最常见、最简单的处理缺失数据的方法是用个案剔除法(listwise deletion),也是很多统计软件(如SPSS和SAS)默认的缺失值处理方法。在这种方法中如果任何一个变量含有缺失数据的话,就把相对应的个案从分析中剔除。如果缺失值所占比例比较小的话,这一方法十分有效。至于具体多大的缺失比例算是“小”比例,专家们意见也存在较大的差距。有学者认为应在5%以下,也有学者认为20%以下即可。然而,这种方法却有很大的局限性。它是以减少样本量来换取信息的完备,会造成资源的大量浪费,丢弃了大量隐藏在这些对象中的信息。在样本量较小的情况下,删除少量对象就足以严重影响到数据的客观性和结果的正确性。因此,当缺失数据所占比例较大,特别是当缺数据非随机分布时,这种方法可能导致数据发生偏离,从而得出错误的结论。
(二)均值替换法(Mean Imputation)
在变量十分重要而所缺失的数据量又较为庞大的时候,个案剔除法就遇到了困难,因为许多有用的数据也同时被剔除。围绕着这一问题,研究者尝试了各种各样的办法。其中的一个方法是均值替换法(mean imputation)。我们将变量的属性分为数值型和非数值型来分别进行处理。如果缺失值是数值型的,就根据该变量在其他所有对象的取值的平均值来填充该缺失的变量值;如果缺失值是非数值型的,就根据统计学中的众数原理,用该变量在其他所有对象的取值次数最多的值来补齐该缺失的变量值。但这种方法会产生有偏估计,所以并不被推崇。均值替换法也是一种简便、快速的缺失数据处理方法。使用均值替换法插补缺失数据,对该变量的均值估计不会产生影响。但这种方法是建立在完全随机缺失(MCAR)的假设之上的,而且会造成变量的方差和标准差变小。
(三)热卡填充法(Hotdecking)
对于一个包含缺失值的变量,热卡填充法在数据库中找到一个与它最相似的对象,然后用这个相似对象的值来进行填充。不同的问题可能会选用不同的标准来对相似进行判定。最常见的是使用相关系数矩阵来确定哪个变量(如变量Y)与缺失值所在变量(如变量X)最相关。然后把所有个案按Y的取值大小进行排序。那么变量X的缺失值就可以用排在缺失值前的那个个案的数据来代替了。与均值替换法相比,利用热卡填充法插补数据后,其变量的标准差与插补前比较接近。但在回归方程中,使用热卡填充法容易使得回归方程的误差增大,参数估计变得不稳定,而且这种方法使用不便,比较耗时。
(四)回归替换法(Regression Imputation)
回归替换法首先需要选择若干个预测缺失值的自变量,然后建立回归方程估计缺失值,即用缺失数据的条件期望值对缺失值进行替换。与前述几种插补方法比较,该方法利用了数据库中尽量多的信息,而且一些统计软件(如Stata)也已经能够直接执行该功能。但该方法也有诸多弊端,第一,这虽然是一个无偏估计,但是却容易忽视随机误差,低估标准差和其他未知性质的测量值,而且这一问题会随着缺失信息的增多而变得更加严重。第二,研究者必须假设存在缺失值所在的变量与其他变量存在线性关系,很多时候这种关系是不存在的。
(五)多重替代法(Multiple Imputation)
多重估算是由Rubin等人于1987年建立起来的一种数据扩充和统计分析方法,作为简单估算的改进产物。首先,多重估算技术用一系列可能的值来替换每一个缺失值,以反映被替换的缺失数据的不确定性。然后,用标准的统计分析过程对多次替换后产生的若干个数据集进行分析。最后,把来自于各个数据集的统计结果进行综合,得到总体参数的估计值。由于多重估算技术并不是用单一的值来替换缺失值,而是试图产生缺失值的一个随机样本,这种方法反映出了由于数据缺失而导致的不确定性,能够产生更加有效的统计推断。结合这种方法,研究者可以比较容易地,在不舍弃任何数据的情况下对缺失数据的未知性质进行推断。NORM统计软件可以较为简便地操作该方法(NORM统计软件可以在http://www.stat.psu.edu/~jls/misoftwa.html可以免费下载)。
三、五种插补方法的实证比较
为了比较这五种缺失值插补方法的不同结果,我们使用实际数据库进行实证研究。数据来源于零点研究咨询集团于2006年秋对云南农村169位农民进行的居民生活调查。我们以此次调查中涉及到的4个变量为例:年龄、收入、精神生活满意度、压力感得分。其中,年龄没有缺失值。收入以“千”为单位,有21%的缺失值。精神生活满意度为6项指标得分之和,总分为30分,有2%的缺失值。压力感得分(本次调查的因变量)为3项指标得分之和,总分为15分,有16%的缺失值。
(一)描述性指标比较
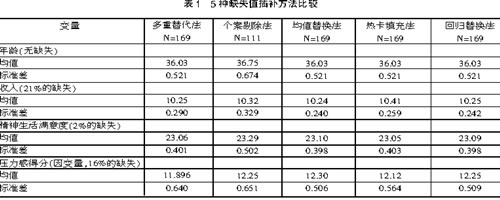
我们首先比较采用5种方法插补后,每个变量的均值和标准差的变化。除了在个案剔除法中有58位个案被剔除之外,其余4种方法都有169个个案参与计算与分析。
从表1中可以发现采用不同的插补方法,其变量的均值和标准差是不同的。当变量的缺失值比较少时(如精神生活满意度),采用5种方法插补后的均值和标准差差异较小。但当缺失值所占比例增大时(如收入、压力感得分),采用不同方法后的均值和标准差差异较大。5种方法中,使用个案剔除法后各变量的标准差都明显增大,使用均值替换法后各变量的标准差都明显减小。
 |
(二)回归分析比较
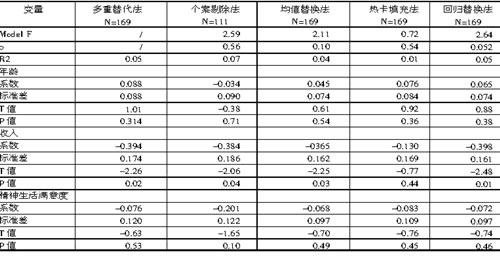
我们以压力感得分为因变量,其余3个变量为自变量进行回归分析。观察表2可以发现,从F值上看,个案剔除法与回归替换法的F值较高。
由于回归分析中,各个变量是相互关联的,所以虽然年龄变量没有缺失值,但由于其他变量存在缺失,导致年龄变量在回归方程中的系数也会发生变化。从表2中可以看出这种变化是比较大的,其中T值从-0.38变化至1.01,与之相应的P值也从0.314变化至0.71。这提醒我们,在进行多元分析时,尤其要注重缺失数据插补方法的使用,因为它不仅会影响到有缺失值的变量,而且影响没有缺失值的变量。
采用不同插补方法对“收入”变量的影响较大。其中,使用热卡填充法后的系数是最大的,并且明显高于了采用其他方法插补后的系数。从P值上看,使用热卡填充法该变量的影响不是显著的,但使用其他插补方法,却可以使得该变量对因变量的影响是显著的。这和前面的分析是一致的,即在回归分析中,用热卡填充法获得的系数是不稳定不可靠的。
 |
应该说上述5种缺失值插补方法各有利弊,研究者在选用插补方法时应该综合考虑缺失数据产生机制、缺失值所占比例、研究能力、时间限制等因素,具体情况具体分析,寻找到在当前条件下最适宜的方法。对于各类插补,共同的目的在于使不完全样本的已有信息得到最佳利用。



